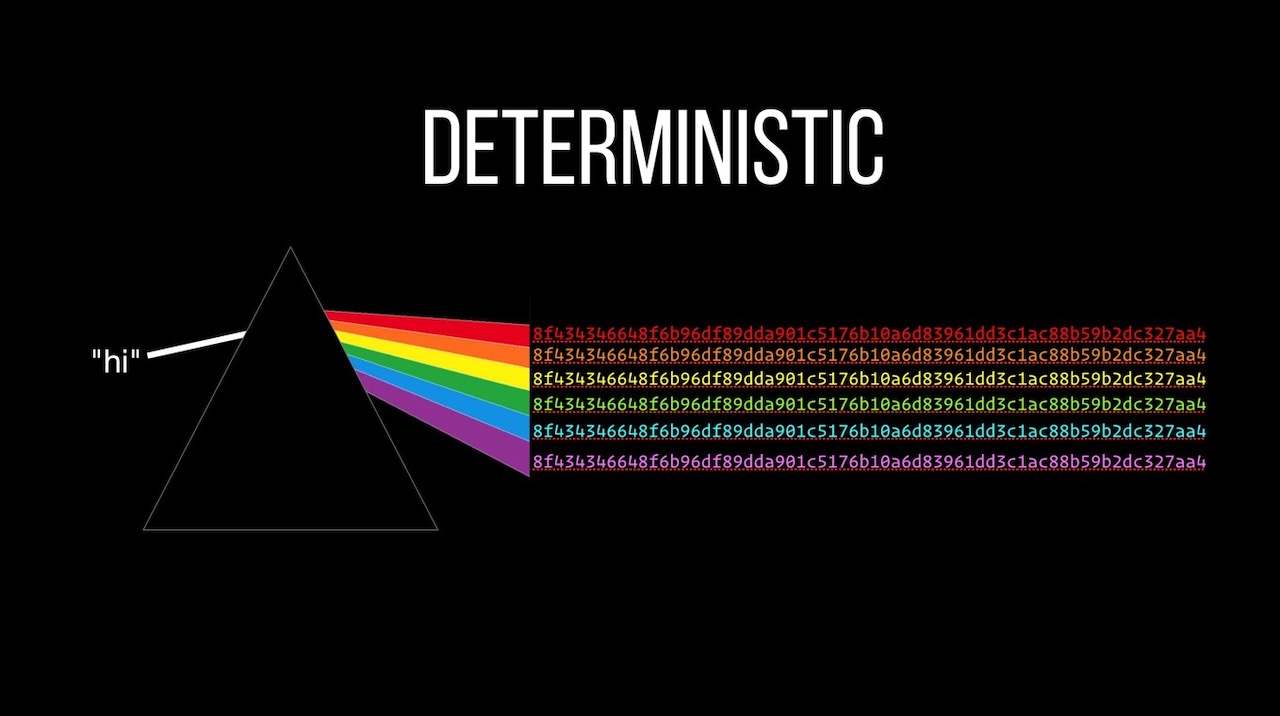
I've used hashes for a long time and had a general understanding of what they do... but that's about it. I knew I needed to hash passwords (and other secure data) if I was going to store them in my database... but that's about all.
I was never sure which algorithms to use nor why... so I dug in and found out. That's the first part of this video.
The second is asymmetric encryption: encoding with a public key and decoding with a second, private key. Absolutely ground-breaking idea! The math is amazingly straightforward too... although I will admit to struggling to explain some of it.
The Code
To produce a simple hash using Node:
const crypto = require("crypto");const hash = crypto.createHash("sha256").update("hi").digest("hex");console.log(hash);Hashing a password with PBKDF2 using a million rounds to slow things down:
const crypto = require("crypto");const hashPassword = function(pw){ return new Promise(function(resolve, reject){ crypto.pbkdf2(pw,"super-secret-salt",1000000,32,"sha512", function(err, buffer){ if(err) reject(err); else resolve(buffer.toString("hex")) }); })}Hashing using scrypt, assigning a cost:
const hashPassword = function(pw){ return new Promise(function(resolve, reject){ crypto.scrypt(pw,"super-secret-salt",32, {cost: 2**14}, function(err, buffer){ if(err) reject(err); else resolve(buffer.toString("hex")) }); })}Creating a checksum using MD5:
const crypto = require("crypto");const fs = require("fs");const data = fs.readFileSync("./message.txt");const checksum = function(data){ return crypto.createHash("md5").update(data, "utf8").digest("hex")}console.log(checksum(data));A super-simple mining operation (meant for demonstration only) for blockchain stuff:
const crypto = require("crypto");const createHash = (block) => { //need to pass a string to our const hashValue = JSON.stringify(block) return crypto.createHash("sha256") .update(hashValue) .digest("base64");}const mine = (block, difficulty = 2) => { let found = false, start = new Date().getTime(); //we're looking for a string of 0s so let's create the pattern //I could use Regex but I'm not that good const lookingFor = "0".padStart(difficulty, "0"); console.log("Looking for a hash starting with", lookingFor); const duration = new Date().getTime() - start; while(!found){ const possibleHash = createHash(block); //does the hash start with zeroes? found = possibleHash.substring(0, difficulty) === lookingFor; if(found){ block.hashKey = possibleHash; return block; } block.nonce += 1; //10 second kill switch if(duration > 10000) return "Didn't find it under 10s" }}const block = { transactions: [ {from: "me", to: "you", amount: 10.00}, {from: "you", to: "me", amount: 5.00} ], timestamp: 1609702546153, //if this changes the hash changes nonce: 0, previousKey: "00RSDThMVcQAvoocD3klO/6pjJ4a8pRbZ3ykk3XXhXE="}//let's see how long this takesconst start = new Date().getTime();//let's do it!const result = mine(block, 4);const duration = new Date().getTime() - start;console.log(`That took duration ${duration}ms`);console.log(result);And finally, our trip through the basics of RSA using super small primes:
//resources//https://www.cs.drexel.edu/~jpopyack/IntroCS/HW/RSAWorksheet.html//https://www.cryptool.org/en/cto/highlights/rsa-step-by-step//let's find two relatively prime numbers, e and d, such that//e % d mod r === 1//this is the cornerstone of RSAvar findEandD = function(r) { //These are common candidates for e, which can be autoset //and typically 65537 is used, but we'll //start small for speed const possibleEs = [3n,5n,17n,257n,65537n] //now, loop over the possible e's so we can find our d for(let e of possibleEs){ //we want to find a coprime for e, so let's factor it //up to r and see if e % r is 1 //if it is, we found our coprime for (let d = 1n; d < r; d++) { const candidate = e * d; if (candidate % r == 1n) return {e: e, d: d}; } } assert.fail("We shouldn't reach this point")}const p = 499n;const q = 491n;assert.notStrictEqual(p,q, "p and q must be different primes");//our public key, Nconst N = p * q;//Euler's totient for deriving r//r = phi(n) = (p-1) * (q-1)const r = (p-1n) * (q-1n);//now we can calculate e and d for our private keyconst {e,d} = findEandD(r);//our messageconst M = 25n;console.log("e",e);console.log("d",d);console.log("N",N);console.log("r",r);console.log("M", M);//the RSA algorithmconst encrypted = M**e % N;const decrypted = encrypted**d % N;console.log("Encrypted",encrypted);console.log("Decrypted",decrypted);Links and Resources
I cite a number of articles in this video - hard not to. But here they are if you want to read more: