One of the most fascinating uses of graphs is in the optimization of path traversal, which can be used in a vast number of calculations.

As mentioned in the previous chapter, graphs can be used to represent all kinds of information:

• A network of any kind. Social (friends) or digital (computers or the internet), for example
• A decision tree
• Contributions from members of any kind to a cause of any kind
• Atomic interactions in physics, chemistry or biology

Navigation between various endpoints - If you apply weighting to the edges or vertices, you can run useful calculations for just about anything. One of the most common is finding the shortest path between two vertices.

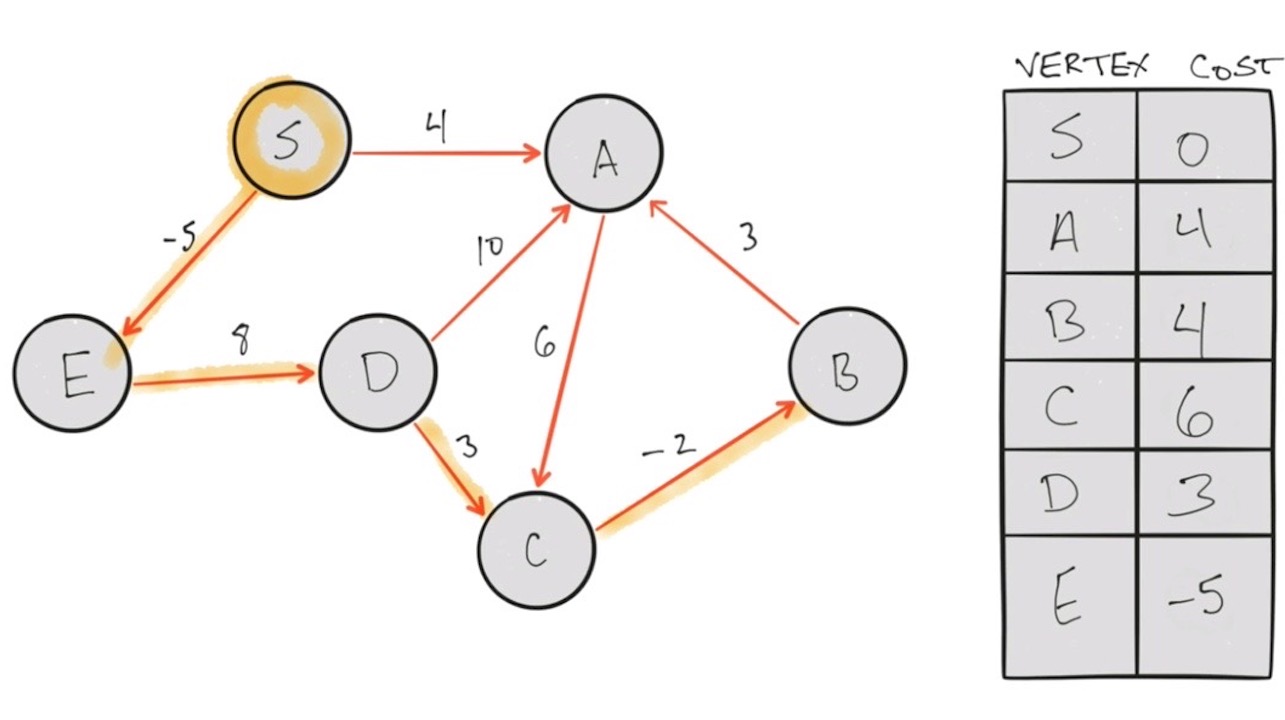
//Bellman-Ford: Shortest path calculation//on an edge-weighted, directed graphconst vertices = ["S", "A", "B", "C", "D", "E"];var memo = {  S:0,  A:Number.POSITIVE_INFINITY,  B:Number.POSITIVE_INFINITY,  C:Number.POSITIVE_INFINITY,  D:Number.POSITIVE_INFINITY,  E:Number.POSITIVE_INFINITY};const graph = [  {from : "S", to : "A", cost: 4},  {from : "S", to :"E", cost: -5},  {from : "A", to :"C", cost: 6},  {from : "B", to :"A", cost: 3},  {from : "C", to :"B", cost: -2},  {from : "D", to :"C", cost: 3},  {from : "D", to :"A", cost: 10},  {from : "E", to: "D", cost: 8}];const iterate = () => {  var doItAgain = false;  for(fromVertex of vertices){    const edges = graph.filter(path => {      return path.from === fromVertex;    });    for(edge of edges){      const potentialCost = memo[edge.from] + edge.cost;      if(potentialCost < memo[edge.to]){        memo[edge.to] = potentialCost;        doItAgain = true;      }    }  }  return doItAgain;}for(vertex of vertices){  if(!iterate()) break;}console.log(memo);