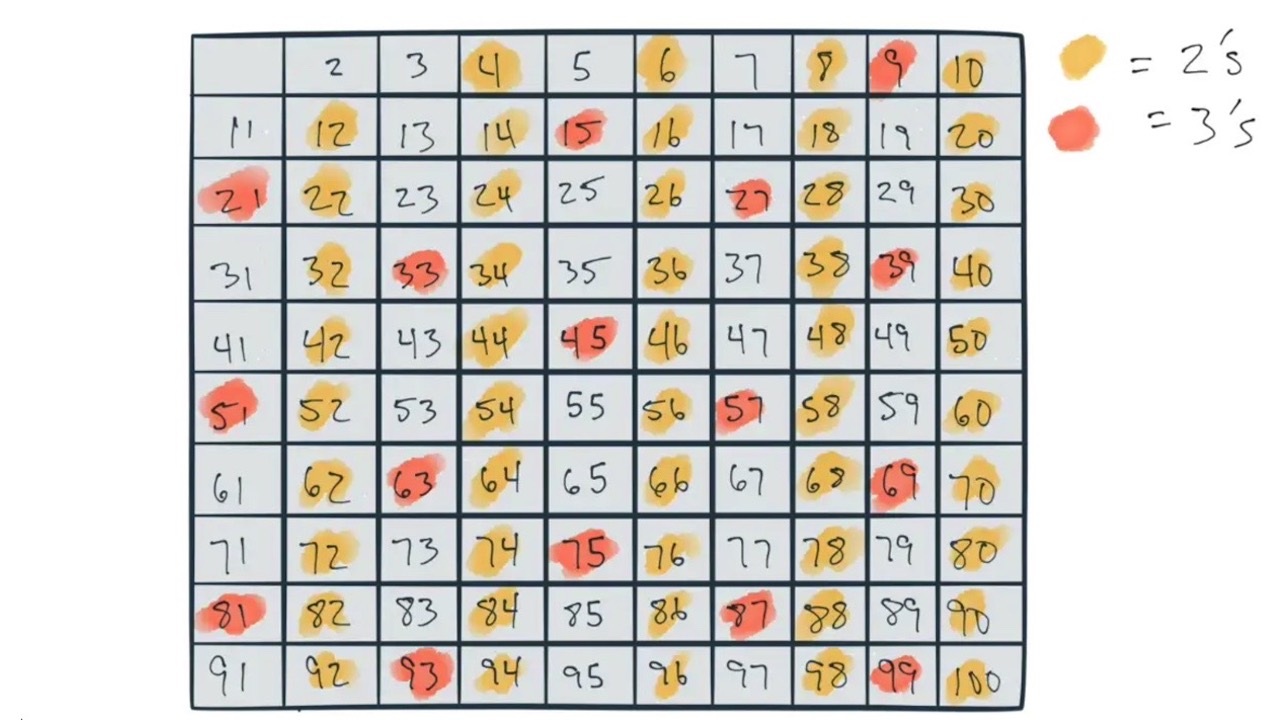
This problem has been solved (rather elegantly I might add) over 2200 years ago by a chap named Eratosthenes. His algorithm is so elegant that just about anyone can understand it. In mathematical terms, his algorithm uses a sieve to filter and extract the numbers in a set:

Sieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The primordial example of a sifted set is the set of prime numbers up to some prescribed limit X.

How would you solve this problem? Also: would you consider this dynamic programming? We’ll answer the latter question at the very end.

The Code

//Sieve of Eratosthenesconst sieve = (n) => {  var grid = {};  for (var i = 2; i <= n; i++) {    grid[i]={marked: false};  }  const limit = Math.sqrt(n);  for (var i = 2; i <= limit; i++) {    for(var x = i + i; x <= n; x += i){      grid[x].marked = true;    }  }  var out =[];  for (var i = 2; i <= n; i++) {    if(!grid[i].marked) out.push(i);  }  return out;};console.log(sieve(100));